It shows a set of properly configured pendulums. When viewed from the side, the brain can recognize different patterns as the bobs swing back and forth at different speed.
The experiment is set up with 15 bobs. The first one is set to do 51 cycles in 60 seconds, the second is set to do 52 cycles in 60 seconds, all the way to the last bob, which is set to do 65 cycles in 60 seconds.
One Pendulum
Let's look at a single pendulum. You bring the bob at a 30° angle, and let it go. It's position over time would be defined as a sine wave.
Two Pendulums
Let's see what happens if you have two pendulums, but they are not synchronized. Pendulum α does 3 cycles in a second, while pendulum β does only 2. Their displacement over time would look like this:
With this graph, we can easily see that at the beginning and at every second, both pendulums are at the left. Also, at 0.5 and 1.5 seconds, pendulum α is at the right, while pendulum β is at the left. This is what our brain recognize as a pattern.
Fifteen Pendulums
Patterns become more apparent with more pendulums, but they can also look more random. The brain recognize when the bobs form groups that are going in the same way, or form a shape (here, this is typically a wave).
The brain seems to have some difficulties to notice patterns made of five groups and more. Forms can also become hard to notice when there is not enough bobs (resolution) to correctly show the wave. For example, when the bobs are first let go in the video, they form a wave of increasing frequency, until, after about 13 or 14 seconds, the brain can't make out the wave anymore.
Mathematics
The most important thing in the experiment is to carefully time the bobs. How to do that? The formula to find a pendulum's cycle (taken from wikipedia, because this was far beyond my skills) is
In the video, the initial angle seems to be around 30°, so we can use this value (and greatly reduce the complexity of the formula). Also, gravity on Earth is 9.80665 m/s^2. That simplifies the formula to
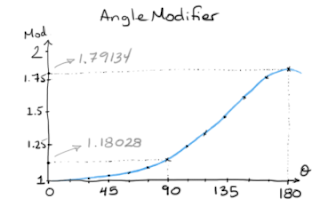
For those who care, the graph of the angle modifier looks like this:
If we want the first bob to oscillate 51 times per minute,
we have to set the length of cord to almost one third of a meter, which is pretty much what we can see in the video. With the same formula, we can find that the quickest bob should have a 0.20448 meter cord.
Furthermore, the dark-blue curve on the graph is the same curve that the bobs make initially in the video. Trivia: for a bob to oscillate once per minute, it would need a cord almost 1 kilometer long. For it to oscillate once per day, the cord would be longer than the distance from the Sun to Saturn.
I have made a small online calculator for such pendulums. You can find it at my web site. At the time of writing, giving the data to find the angle is not implemented (I will have to code a brute-force algorithm for that, or an approximation), but you can easily find the other data.







No comments:
Post a Comment